Hyperbolic Geometry refutes Euclid's fifth postulate by saying that given line l and point p, there are an infinite number of lines through p parallel to l. This type of geometry is very tough to visualize, and that is one of the reasons that it took so long to be discovered.
In Hyperbolic Geometry, there are an infinite number of lines parralel to a given line. In addition, the measure of the angles in a triangle is always less than 180 degrees.
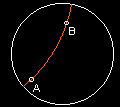
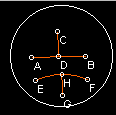
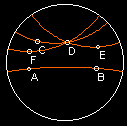
| 1: 2 Points determine a line | 2: A straight line can be extended without limitation | 3: Given a point and a distance a circle can be drawn with the point as center and the distance as radius | 4: All right angles are equal | 5: The Parralel Postulate |
|
|
|
|
|
| Here, it is shown that points A and B determine line AB | Here, AB goes to the edge of the boundary circle, showing that it is infinite | This circle was constructed by setting the point and a length for the radius (by picking another point). | Here, these two angles both measure 90 degrees and are thus right and equal | Here, lines CD, ED, and FD are all parralel to AB and pass through D, proving that given a line and a point not on a line , there are an infinte number of parralel lines through that point. |
Given that hyperbolic geometry is so hard to visualize, there are several different representations of it. Two that are particularly useful are known as the Poincare Disk and the Upper Half Plane
The Poincare Disk represents the hyperbolic plane by "shrinking" it to fit within a boundary circle. It shrinks it in such a way that it is equivalent to the original, however. In other words, as you approach the boundary circle, things get bigger. Any line touching the boundary circle is an infinite line. The following triangle was constructed using NonEuclid software, which uses the Poincare Disk representation.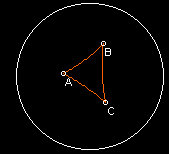 
. In this particular triangle, the sum of the measures of the angles is 132 degrees. In the Hyperbolic Geometry Exhibit there is a nice Java simulation of the Poincare Disk. In addition, you can Draw your own figures in the Poincare Disk
The Upper Half Plane represents the Hyperbolic plane in the following way: The plane is the upper half of the x-y coordinate system with the boundary being the x-axis (y must be >0). In this system, lines are either half-circles that intercept the x-axis, or lines perpindicular to the x-axis. While this is easier to represent, it has the flaw that it does not represent distance accurately. Its probelm is similar to the problem that occurs when you try and make a flat map of the world: distance is distorted.Try a java simulation of the Upper Half Plane